在车间里,通常会根据库存水平寻找到瓶颈。如果缓冲库存是满的,瓶颈就在缓冲的下游。如果缓冲库存是空的,那么瓶颈就在缓冲库存的上游。这是真的吗?我的学生Carolin Romeser和我花了不少时间来验证这一点,并发现了一些有趣的结果。一般来说,这是真的,但是……一切在细节中。
在车间里,通常会根据库存水平寻找到瓶颈。如果缓冲库存是满的,瓶颈就在缓冲的下游。如果缓冲库存是空的,那么瓶颈就在缓冲库存的上游。这是真的吗?我的学生Carolin Romeser和我花了不少时间来验证这一点,并发现了一些有趣的结果。一般来说,这是真的,但是……一切在细节中。
简介
首先,我们需要准确地定义下瓶颈:
瓶颈是影响整个系统产出的工序。影响越大,瓶颈就越严重。
在一个生产系统(也可以是其他系统)中,如果瓶颈在下游,缓冲库存就会被填满,如果瓶颈在上游,缓冲库存就会被清空,如下图a)和b)所示。瓶颈是原因,缓冲库存是结果。 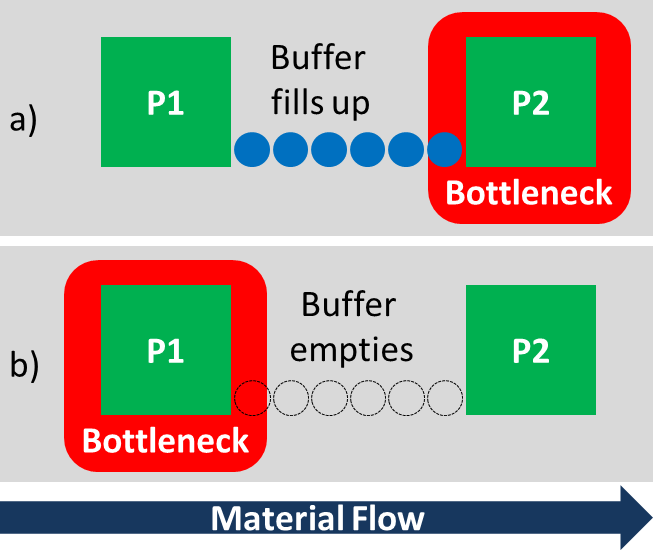
在工业界以及许多学术论文和方法(也包括我自己的方法)中,这种关系通常被用来寻找瓶颈:
- 如果缓冲库存是(相当)空的,那么瓶颈一定是(可能)在上游。
- 如果缓冲库存是(相当)满的,那么瓶颈一定是(可能)在下游。
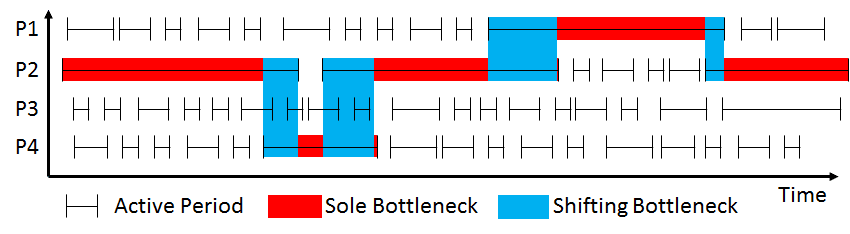
当然很容易想象出与上述描述不符的例子。以下面的例子为例,首先工序P1是瓶颈,其后的缓冲库存是空的。如果瓶颈转移到P2,P1后面的缓冲库存开始填满。现在假设缓冲库存刚填满,瓶颈又转移回P1!这种情况下,工序P1是永远不需要等待P2的。 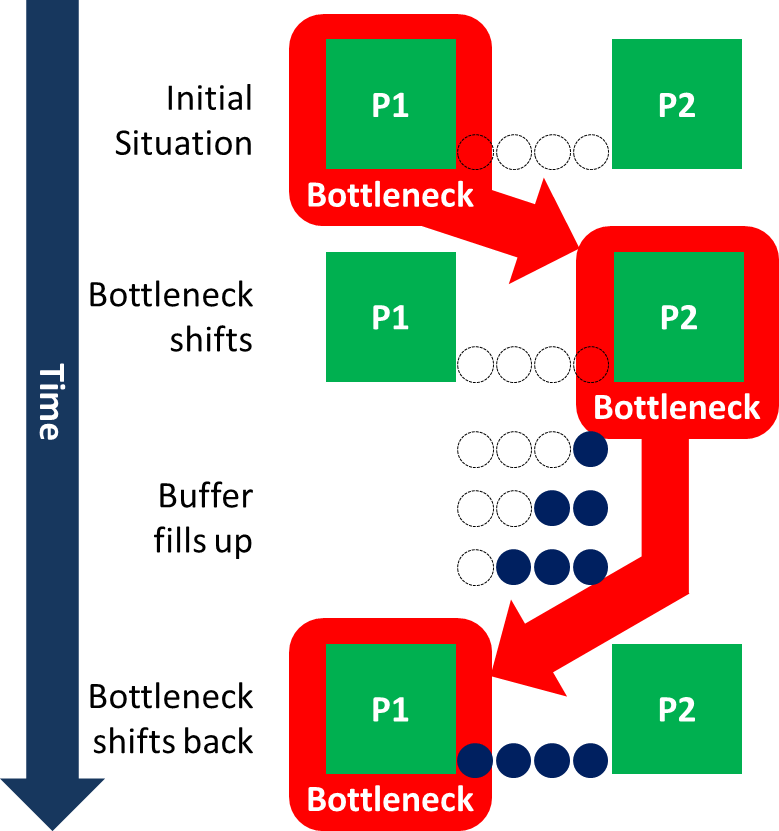 我把上面的瓶颈工序标示出来。但根据我们上面对瓶颈的定义,瓶颈必须影响系统的整体产出速度。但在上面的例子中,影响整个系统的总是P1。就在P2将产生影响之前,瓶颈又转移回了P1。 尽管缓冲库存完全满了,但P2实际上从来都不是瓶颈。
我把上面的瓶颈工序标示出来。但根据我们上面对瓶颈的定义,瓶颈必须影响系统的整体产出速度。但在上面的例子中,影响整个系统的总是P1。就在P2将产生影响之前,瓶颈又转移回了P1。 尽管缓冲库存完全满了,但P2实际上从来都不是瓶颈。
当然,这是一个极端的情况,但也是很有可能的发生的。因此,即使在缓冲库存完全满或空的情况下,也不能肯定地说瓶颈在哪里,只能说是一种概率。
理论期望
从理论上讲,你会发现瓶颈在上游或下游的概率与库存水平直接相关。如果缓冲库存是满的,几乎可以肯定,瓶颈在下游。如果缓冲库存是空的,几乎可以肯定,瓶颈在上游。对于两者之间的任何库存水平,你都有一个线性关系。如果缓冲库存正好满了50%,那么瓶颈可能在上游或下游。 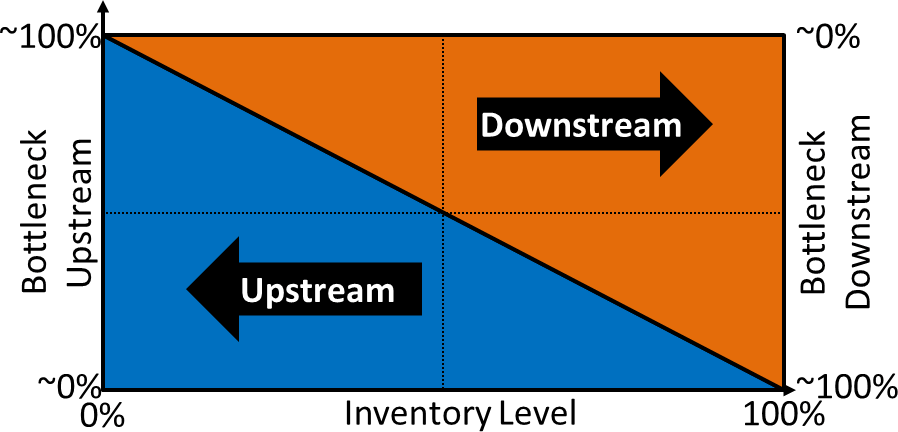
衡量标准:活跃期法
尽管找了很多文献,但我们并没有发现任何通过库存识别瓶颈的研究。工业界和学术界很多人都用这个假设来寻找瓶颈,但到目前为止,还没有人确认过这种方法是否正确。因此,我们开始测试这一假设。
这里面有一个难题,为了检验库存水平和瓶颈方向的关系,需要找到瞬时转移的瓶颈。大多数方法本身又是用这种库存关系来寻找瓶颈的。因此,这就是用自己的方法验证自己的工具,当然不证自明。
我自己开发了一种识别转移瓶颈的替代方法:活跃期法(在我的文章《数学方法精确识别瓶颈2–活跃期法》中有相关内容):
- 如果工序等待另一个工序,则该工序不活跃
- 否则,工序被认为在活跃期
- 具有最长的不间断活跃期的工序是此时的瓶颈
- 两个长时间段的重叠表示瓶颈正在转移
现在,我们可以说瓶颈在哪里,或者瓶颈是否正在转移。
仿真系统
我们使用了一个简单的模拟系统,它具有无限的供应和需求,两个节拍时间随机的工序,以及中间的缓冲库存。  我们运行模拟并记录了缓冲库存水平以及瓶颈工序的情况。事实上,我们对许多不同的系统重复了这一过程,例如,不同的平均节拍时间(从相同的节拍时间,到一个工序的节拍时间是另一个工序的20%),不同的随机分布(指数、埃朗……)和不同的缓冲库存水平(容量从3个到100个)。
我们运行模拟并记录了缓冲库存水平以及瓶颈工序的情况。事实上,我们对许多不同的系统重复了这一过程,例如,不同的平均节拍时间(从相同的节拍时间,到一个工序的节拍时间是另一个工序的20%),不同的随机分布(指数、埃朗……)和不同的缓冲库存水平(容量从3个到100个)。
对称系统
对于一个对称系统,两个工序的节拍时间相近,仿真结果与理论结果非常接近。下面是一个系统的结果,该系统有两个相同指数分布的节拍时间,缓冲库存容量为10。还显示了置信区间。 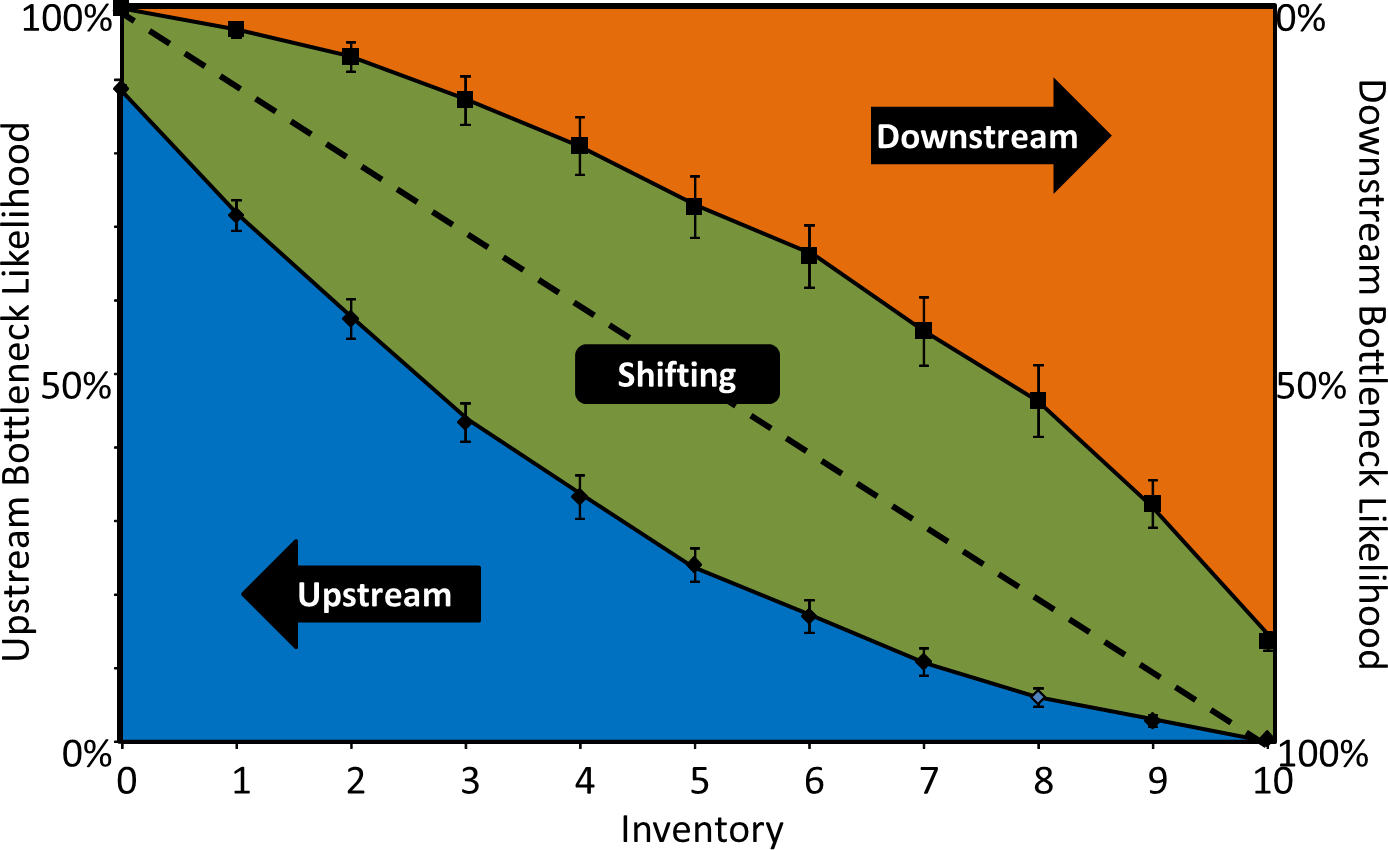 结果与预期一致。如果缓冲库存趋向于0,那么更有可能(但不确定)瓶颈在上游。同样,如果缓冲库存趋于满,则更有可能(但不确定)瓶颈在下游。由于活跃期方法有时会有一个转移期,我们并不总是知道瓶颈在哪。中间的绿色区域代表这个转移期。
结果与预期一致。如果缓冲库存趋向于0,那么更有可能(但不确定)瓶颈在上游。同样,如果缓冲库存趋于满,则更有可能(但不确定)瓶颈在下游。由于活跃期方法有时会有一个转移期,我们并不总是知道瓶颈在哪。中间的绿色区域代表这个转移期。
因此,如果在缓冲库存中有2个零件,那么就有~55%的概率,瓶颈在上游,还有~7%的概率,瓶颈在下游,剩下的~38%的概率,由于瓶颈正在转移,我们不知道库存结果,绿色部分表示瓶颈转移。
你会说,假设得到了证实吗?没有那么快!
不平衡系统
我们还用不平衡系统进行了模拟实验,其中一个工序比另一个工序快。现在,我们的理论模型被打破了。下面是模拟结果,其中P1工序的节拍时间是P2的20%,因此P1要快得多。 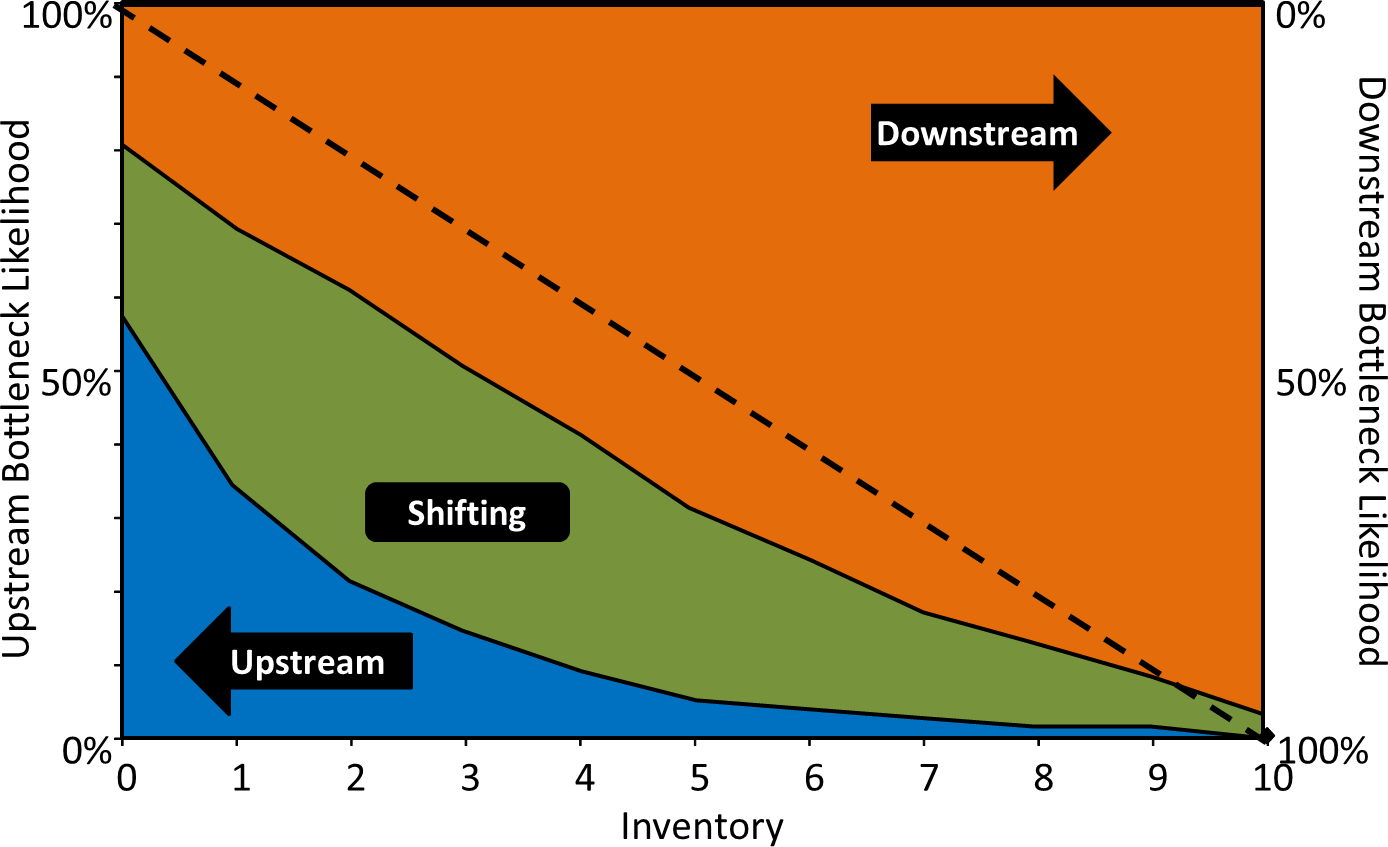 很明显,这不再是对称的了。不管库存是多少,瓶颈几乎总是在下游。以库存水平为2为例,与对称系统相比,不如说是只有20%左右瓶颈在上游的概率,以及40%瓶颈在下游的概率(剩下的40%概率瓶颈是在转移的)。无论库存水平如何,在这个不平衡例子中,瓶颈更可能是在下游。因此,瓶颈方向与库存呈线性关系的假设并不成立!
很明显,这不再是对称的了。不管库存是多少,瓶颈几乎总是在下游。以库存水平为2为例,与对称系统相比,不如说是只有20%左右瓶颈在上游的概率,以及40%瓶颈在下游的概率(剩下的40%概率瓶颈是在转移的)。无论库存水平如何,在这个不平衡例子中,瓶颈更可能是在下游。因此,瓶颈方向与库存呈线性关系的假设并不成立!
这意味着什么呢?
总言之,对于节拍时间接近的系统,你可以用库存水平来寻找瓶颈,效果最好。对于节拍时间差别很大的系统,它的效果并不好。
这的确也很无奈。通过库存来寻找瓶颈,实在是非常方便。幸运的是,有一个方式,如果一个工序是比其他工序更严重的瓶颈,那么大多数时候,库存方法还是会指向这个严重瓶颈。
以上面那张不平衡的图为例。这张图显示了瓶颈方向的可能性,但没有显示库存水平实际发生的频率。事实上,花了相当长的时间模拟,甚至有几次库存水平为0和1,大部分时间的库存水平都在8到10之间。
因此,仍然可以通过库存水平找到瓶颈,只是不应该只依赖一个观察结果! 现在,走出去,看看你的库存,找到你的瓶颈,组织你的行业!
参考资料
- Romeser, Carolin: “Richtung des Engpasses in Abhängigkeit vom Füllstand eines Bestandes”, Master Thesis Karlsruhe University of Applied Sciences, October 6th 2015.
- Romeser, Carolin., Roser, Christoph. Direction of the Bottleneck in Dependence on Inventory Levels, in: Proceedings of the International Conference on the Advances in Production Management System. Presented at the International Conference on the Advances in Production Management System, Iguassu Falls, Brazil, 2016.
Translated by Xie Xuan