The Power of Six: Relation between Time and Money in Manufacturing

Time is money. You know that. But with respect to product cost and lead time, there is a rule of thumb that estimates this relation. Let me present to you the “Power of Six,” discovered by Rajan Suri. This gives you a rough estimate of how the lead time of your products influences the cost and vice versa. This first post looks at the original work, and my next post applies this rule also to segments of the value stream.

Introduction

One very big aspect of manufacturing is time. How fast can you get your products to the customer (i.e., what is the delay between the order of the customer and the delivery to the customer)?

This metric has a huge impact on the success of a company. Usually, customers like to get their stuff fast, and a faster delivery often increases customer satisfaction.

There are even a number of different overlapping terms for this time. The lead time is usually from the start of production till completion. The replenishment time is the time to replace a consumed item in your inventory. The turnaround time or response time is the time between a customer order and the delivery of this item.

However, what is less known is that a faster response time also usually decreases cost. If you have a faster response time, then you probably have less inventory, less fluctuation, less handling, and many other expenses. Hence, on average, being faster reduces your production cost. The Power of Six gives an estimate of this relation.

Traditional cost accounting has difficulties with this. They cannot estimate the effect of reduced fluctuations, and see only parts of the effect of reduced inventory. Accountants take the easy way out by considering anything they do not know as zero. Hence, for them, reducing fluctuations, etc. holds no value – which is clearly wrong. For more on this see my post The Problems of Cost Accounting with Lean.

Time and Money

There are two elements that the Power of Six brings into relation. The first one is the turnaround time, the second one is product cost.

The Power of Six originated with Quick Response Manufacturing (QRM). One key metric is the Manufacturing Critical Path Time (MCT). Since the MCT is used for quite a few different things, it has a very detailed definition. The definition is:

Manufacturing Critical Path Time MCT: The typical amount of calendar time from when a customer submits an order, through the critical path, until the first end item of that order is delivered to the customer.

For our purposes, however, we can simplify this to the average time between receiving an order and delivering the (first part of the) order to the customer. This is based on real time, not working time, and includes for example all off-shifts, weekends, plant holidays, etc. You could for example take the average days between receiving the order and delivery. Do not take only rush orders, as this will be a biased sample and will be far from your average duration. It is important that this includes the entire value chain. If you fulfill a customer order merely by grabbing the make-to-stock item from the shelf, this rule of thumb won’t work.

The cost is simply the total product cost including overhead, materials, and everything else.

The Power of Six

Assume you want to reduce your cost by reducing your turnaround time (or MCT). Let’s assume you have the following variables:

• C₀ is the current product cost
• C₁ is the desired new product cost
• T₀ is the current turnaround time
• T₁ is the new turnaround time needed

The relation according to the power of six is as follows:

\[ { \frac{T_1}{T_0} = ( \frac{C_1}{C_0})^6}\]

and that is it. If you have a desired cost reduction, then you can simply calculate the needed percentage reduction of your turnaround time. For example, if you want to reduce your cost by 5% (i.e., reduce it to 95% of your previous cost), your formula would be

\[ { \frac{T_1}{T_0} = ( \frac{C_1}{C_0}) ^6 = ( \frac{95\%}{100\%}) ^6 =  (95\%) ^6 = 74\%}\]

Hence you can estimate that you would have to reduce your turnaround time by around 26% (i.e., to 74% of the original value) to achieve a 5% cost saving, assuming you only influence the turnaround time and no other cost saving levers.

It would also work if you start with the reduction of the turnaround time. Assuming you re-shore supply from China back to the USA, your turnaround time would reduce by three months shipping time from eight months to five months. You can turn the formula around as shown below by not taking the ratio of the costs to the power of six, but the ratio of the times to the power of 1/6th.

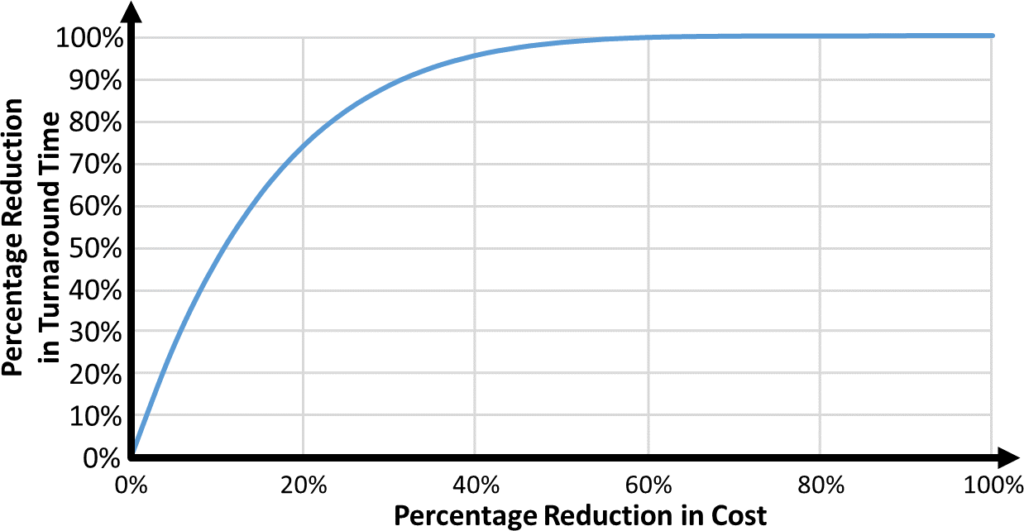
\[ { \frac{C_1}{C_0}=(\frac{T_1}{T_0})^ \frac{1}{6}=(\frac{5}{8})^ \frac{1}{6}= 63\%^ \frac{1}{6}=92\%}\]

Hence, if you reduce your turnaround time by 38% to 63%, you would reduce your cost by around 8% to 92% of the previous cost. The overall relation is shown in the graph below (albeit I presume the prediction becomes less accurate as your improvements approach 100%).

By the way, it also works the other way round. If you outsource some production to China, you extend your supply chain by three months. Let’s do the calculation, assuming you go from a three-month turnaround to a six-month turnaround time you increase your turnaround time to 200%:

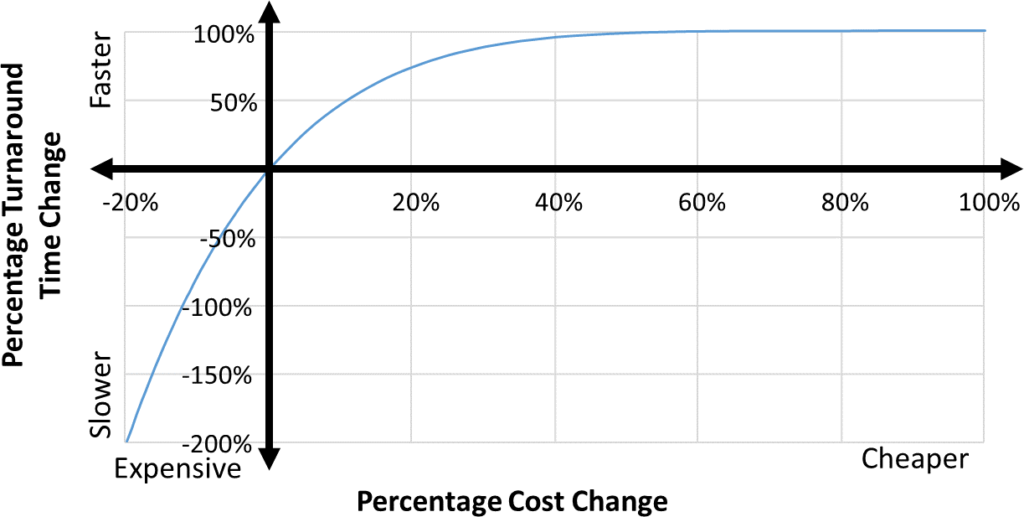
\[ { \frac{C_1}{C_0}=(\frac{T_1}{T_0})^ \frac{1}{6}=(\frac{6}{3})^ \frac{1}{6}= 200\%^ \frac{1}{6}=112\%}\]

Hence by doubling your turnaround time, the cost would increase to 112% of the  cost, an increase of 12%. Therefore, production in China would have to be at least 10.7% cheaper just to break even. (Different number because the way percentages work. If you increase 100€ by 12% you get 112€. Decreasing 112€ by 12% would give you 98.56€. Decreasing it by 10.7% would give you 100€ again.) The graph below is an extension of the graph above continuing the relationship if you make the turnaround time worse.

Accuracy of the Power of Six

This rule is a rough rule of thumb. To show you the accuracy, I have plotted the raw data below from the original paper from Tubino and Suri 2000 (full source below). This is to give you a feeling of the underlying change, but is by no means an accurate estimate of the performance after the improvements.

This original Power of Six rule applies to the entire value stream. However, by extrapolation it should also work for segments of the value stream. I will talk about this in more detail in my next post. Until then, go out, reduce your lead time, and organize your industry!

P.S.: Many thanks to Rajan Suri for his input and help, and of course for finding this relation in the first place!

Sources

• Suri, Rajan. It’s About Time: The Competitive Advantage of Quick Response Manufacturing. 1 edition. New York: Productivity Press, 2010. Pages 165–167.
• Suri, Rajan. MCT Quick Reference Guide. Suri Consulting and Seminars, LLC, 2014. Page 11.
• Tubino, Francisco, and Rajan Suri. “What Kind of ‘Numbers’ Can a Company Expect After Implementing Quick Response Manufacturing? – Empirical Data from Several Projects on Lead Time Reduction.” In Quick Response Manufacturing 2000 Conference Proceedings, 2000.